Stellar Birth
Overview
The overriding idea behind the birth of stars is the collapse of material into a more compact form. When material compresses, it heats up (like when inflating a bicycle tire). If it gets hot enough and the pressures are large enough, then nuclear fusion will begin and a new star is born.
Gravitational Collapse
The first step in the birth of a star is to wait. Dust, gas, and other materials sit around in nebulae, and it waits for eons until a passing star, shockwave, or other gravitational disturbance passes through or by the nebula.
Once this happens, the interloper's gravity causes swirls and ripples of changing density. It would be like spreading marbles out on a trampoline, and then rolling a large lead ball around the edge, or through the middle. The other marbles would roll around, and clump together near the path the lead one took. It is no different in a nebula when a star passes by. To add to the marble analogy: When the marbles gather in places, the dip in the trampoline causes other marbles to accumulate in the same spot until there are just a few separate piles of marbles, with very few marbles in between. This process is called accretion, and causes the stars - or marble clusters - to grow larger.
However, the molecules in the nebula have energy of their own because of their heat, and this resists collapse. The cloud will only collapse if its mass is large enough to overpower the individual motions of the molecules - this critical mass called the "Jean's Mass." This is derived from the Virial Theorem:
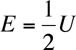
Rearranging it, and substituting in the equations for kinetic an potential energy, the equation becomes:
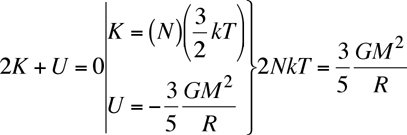
In the above equation, K is the kinetic energy, U is the potential energy, N is the number of molecules, k is Boltzmann's Constant, T is temperature, G is the gravitational constant, M is the mass, and R is radius.
Now, the number of particles in the cloud is equal to the mass of the cloud divided by the mass of the particles, N = M/m. Assuming that the cloud has a constant density (ρ), you can relate its size to its mass by the equation below:
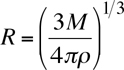
Rearranging, combining, and simplifying, we get the equation for Jean's Mass, MJ:
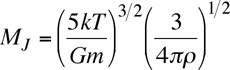
If the cloud's mass is larger than this critical mass (which is a function of temperature, mass of the molecules, and overall density), then it will collapse. Otherwise, it will continue to swirl and clump, but the clumps will not be permanent, and they will dissolve in the cloud.
If it is above the Jean's mass, then the clumps of matter continue to group together in the nebula until they are gigantic clumps of dust and gas. By this time, the clumps have reached sun-like sizes, and by that stage, the gas is dense enough that it will no longer lose heat to the surrounding nebula.
It has become "adiabatically opaque," and the heat that it generates is retained, and it starts to heat up. At this stage, the clump is called a "protostar." From the start of the collapse to this stage, typical time scales are on the order of a few hundred thousand years.
Protostars - Pre-Main Sequence
As the protostar becomes larger, gravity squeezes it tighter, causing pressure to build and for the heat to increase. If you have ever pumped a bicycle tire, you know that when the air becomes compressed, it becomes hotter, as shown in the Ideal Gas Law:
![]()
In this Law, P is pressure, V is volume, N is the number of molecules, k is a constant, and T is temperature. So if pressure is increased, then temperature will correspondingly increase.
On the Hertzsprung-Russell Diagram, the large swath of stars through the center is called the "Main Sequence," and it is where most stars live most of their lives. There is a period of time between when protostars form and when they reach the main sequence, and this is called the "pre-main sequence."
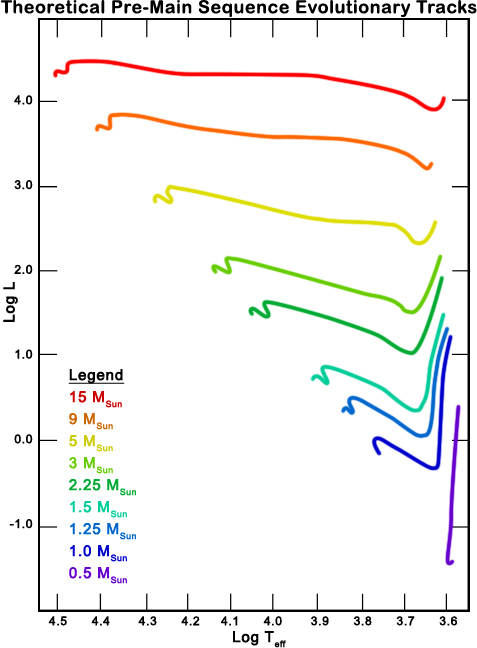 |
| On an H-R diagram with luminosity on the vertical and temperature on the horizontal axes, this shows the results of computer simulations that model the collapse of stellar nebulae to form stars of different masses. The stars start at the far right of the diagram - low temperatures, and travel to the left, increasing in temperature. They all end on a diagonal line that is known as the Zero-Age Main Sequence (ZAMS). |
The pre-main sequence stellar evolution in terms of temperature and luminosity is shown above for a range of stellar masses. Low-mass stars contract and drop in luminosity until the interior opacity drops and the energy comes flooding out, resulting in an increase in surface temperature and luminosity. High mass stars have low opacity to begin with due to high temperatures, and simply heat up as the contract, becoming more luminous in the process.
When the pressure in the center causes the core to reach a temperature of about 10,000,000 K (18,000,000 °F), hydrogen fusion is initiated. Now, the protostar has become a bona fide star. It shines with its own light produced through fusion instead of gravitational contraction. Its solar wind quickly pushes away and photodisintegrates the rest of the dust and gas in its vicinity. It is now known as a "Zero-Age Main Sequence" star, or a ZAMS star.