Finding Exoplanets
Overview
Exoplanets are planets that are outside of our solar system, generally orbiting another star. When astronomers look at objects outside of the solar system, they have to be very large in order to be seen. Only a very few stars other than our own have ever been resolved into disks.
Because we do not yet have the technology to even resolve most stars, astronomers usually have to use other, indirect means to detect and study planets around other stars. To-date, there are six different techniques that are used, and each of these is discussed below.
History
The first known exoplanets were discovered around pulsar stars in the early 1990s (see Wolszczan & Frail (1992)). The reason that these were the first is that it is much easier to use pulsar timing to detect planets than it is to use other methods, such as radial velocity.
However, just a few years later, the first exoplanet orbiting a Sun-like star was found (orbiting 51 Peg, the 51st brightest star in the constellation Pegasus) by Mayor & Queloz (1995), who found it using the radial velocity technique.
Since that time, the number of known extrasolar planets has increased, and presently there are over 300 known to exist. At present, there are six different methods for finding these objects, while new methods are currently being developed in the constant search for a planet like our own.
Method: Astrometry
This is a very difficult method to use to detect planets, and to-date, fewer than a dozen planets have been discovered using it.
The basic concept behind this technique is that every object in the Universe exerts a gravitational pull on every other object. Earth pulls on you and you pull on Earth. The Sun pulls on Earth and Earth pulls on the Sun. But the reason that when you jump Earth doesn't follow you - rather you are pulled back down to Earth - is that the more mass an object has, the greater the gravitational force is exerted. Isaac Newton expressed this in his Universal Law of Gravitation:
![]()
In that equation, Fg is the force of gravitational acceleration, G is the gravitational constant, M is the mass of the larger object, m is the mass of the smaller object, and r is the distance separating the two. Because Earth is so much more massive than you are (by about 1023), you are a fairly meaningless when it comes to exerting a force on Earth.
However, from this equation, you can see that if the two masses are closer, then the affect of the smaller on the larger will be greater. In other words, if you have a large planet tugging on a small star, that planet may be able to produce a noticeable "wobble" in the star.
If we could directly observe that wobble, tracking the star's position very precisely over time, then we could have evidence for a planet being around the star. This is the basis for the Astrometry technique.
As for most methods for discovering exoplanets, the bigger the planet is and the closer it is to its parent star, the more bigger the gravitational effects will be, making it easier for us to detect.
Method: Radial Velocity (AKA Doppler Shift)
This is by far the most commonly used method to detect extrasolar planets. So far, over 85% of all known extrasolar planets have been detected by this method. This is also the method used to detect the first planet orbiting a Sun-like star (in 1995; see Mayor & Queloz (1995)).
It picks up where the astrometry technique left off. Much more often than not, the wobble that the planet induces on the star is too little and the system too far away to directly observe. So astronomers use an indirect method to observe the wobble: The color of light.
One way to think about light is to think about it like sound - as a wave. If you've ever been near a train as it goes by, as it passes you you will hear its whistle drop in pitch. The same thing is true as cars go by - as they approach you, the noise is a slightly higher pitch than when they go away from you.
This because, as a wave, when the car or train is coming towards you the wave is compressed. With sound, this means it's a higher pitch. As the car or train is going away from you, the wave is expanded (rarified). With sound, this means a lower pitch. But, the same thing can be said for light. If an object is emitting light and it is moving towards you, the light waves are compressed, and they appear bluer. If the object is emitting light and it is moving away from you, the light waves are expanded, and they appear redder. This phenomenon is known as Doppler Shift.
Now we can apply this concept to a planetary system, with a planet pulling on its parent star. When the planet is moving away from us, it pulls its star with it, away from us. When the planet is moving towards us, it pulls its star with it, towards us. This will shift the star's light from normal to blue to normal to red and then repeat. It will do this in a very regular and observable manner.
Astronomers use devices called spectroscopes to split light into many colors, like a prism. If they see these shifts in color that repeat in a regular pattern, they they have likely discovered a planet.
As for most methods for discovering exoplanets, the bigger the planet is and the closer it is to its parent star, the more bigger the gravitational effects will be, making it easier for us to detect.
Method: Transit
The transit technique relies heavily upon luck: The planet's orbit must be lined up just right so that its passes directly in front of its parent star as seen from Earth. If this happens, then part of the star's light will be blocked by the planet, and it will appear as though the star has momentarily dimmed. In other words, the planet has eclipsed part of the star. This is another case where the closer the planet is to its star and the bigger the planet is, the more light it will block and the more often it will block it, hence the more likely we are of finding it.
This is an incredibly important method for finding planets because the star's light is only blocked by the solid, opaque part of the planet. If the planet has a large atmosphere, then part of the star's light will filter through the planet's atmosphere. As it passes through the planet's atmosphere, certain parts of it may be absorbed by atoms and molecules, and then those colors will be absent when the light is detected by Earth. Through this, parts of the composition of a few extrasolar planetary atmospheres have been determined.
Method: Direct Imaging
Direct Imaging is probably the simplest, most obvious, and yet the hardest method of finding planets. To-date, less than half a dozen have been found using this method.
The description of it is simple: Point your telescope at a star and see if you find a planet. However, for the reasons described in the Overview of this page, the physical size of the planets are so small, and their light is so dim when compared to their parent star that they are all but invisible if they are there.
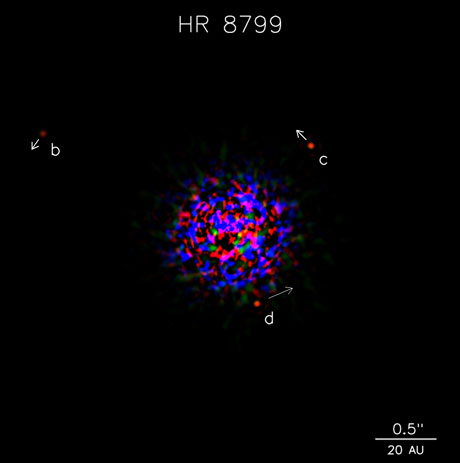 |
| Image of the planetary system around HR 8799, taken via an adaptive optics system on the Keck and Gemini telescopes on Mauna Kea. The star is 1.5x the mass of our sun. The planets labeled "d" and "c" have masses 10x Jupiter's, and "b" has a mass 7x Jupiter's. Image is courtesy of Keck. |
When doing this, astronomers generally search infrared light because (1) stars are dimmer in infrared light, emitting most of their luminosity in the visible wavelengths; and (2) planets are brighter in infrared light.
On November 13, 2008, the Keck Observatory on top of Mauna Kea, HI (USA), announced that they had taken the first photographs of a multiple-planetary solar system around another star. They did not discover the planets - it had already been known that they existed. However, this was a significant milestone in the imaging of exoplanet systems. The discovery photograph is on the right.
Imaging the planets directly allows them to be studied in more details; with their light separated from their parent star's spectroscopy can be used to study the composition of these planets, as well as their temperature and other properties.
Method: Microlensing
This technique is also a fairly rare method used to detect exoplanets, with fewer than a dozen known exoplanets having been found to-date with this method. It relies upon an interesting consequence of General Relativity:
Einstein's General Relativity lets us think of gravity not as a force that pulls objects (like Newton's concept), but rather as something that physically will bend space around it. On Earth, we have been using something like this as a magnifier for over 400 years: A lens. A lens acts to bend light to a focus point, allowing us to magnify something. In much the same way, Einstein predicted that a massive object can bend space around it and magnify objects behind it.
This has been observed to be true many times in astronomy, and it has been put to work in detecting exoplanets. The basic idea is exactly as explained in the paragraph above: A foreground star (one that's relatively close by) passes either directly or almost directly in front of a background star. This will magnify the light from the background star. If that background star has a planet, then it will slightly alter the predicted increase in light of the background star, allowing astronomers to detect it.
Most planets that have been detected in this manner come from the OGLE survey, which is an acronym for the Optical Gravitational Lensing Experiment. The stated goal of OGLE is to be a long-term project with "the main goal of searching for the dark matter with microlensing phenomena." In practice, they observe many stars over the course of many nights over many years in order to search for the microlensing events. This provides a wealth of data that can be used for other purposes, such as microlensing events related to planets.
Method: Pulsar Timing
The pulsar timing method is very similar to the radial velocity and astrometry techniques in regards to their theory, but it is very different from them in practicality. Briefly, pulsars are a special type of dead star that emit beams of radio pulses with extraordinary regularity. For more information, see "Journey Through the Galaxy's" section on pulsars.
The regularity of pulsar's pulses of radio waves is one of the most predictable things in the Universe, and as such, any deviation - no matter how small - means that something else is going on.
In the early 1990s, different teams of astronomers were observing pulsars and discovered that a few of them, while regular, showed periodic shifts of faster pulses and slower pulses (seen in PSR1829-10 for Bailes, Lyne, & Shemar (1991); and PSR1257+12 for Wolszczan & Frail (1992)). Eventually, the teams interpreted these slow-downs and speed-ups as a planet's (or planets' in the case of Wolszczan & Frail) gravity pulling the pulsar away from Earth (like a redshift for the radial velocity method) and towards Earth (like a blueshift for the radial velocity method). And hence the first extrasolar planets were found.
Deriving Planetary Properties
Period: The period - or the planet's "year" - is the easiest property to determine of a planet. For the astrometric, radial velocity, transit, microlensing, and pulsar timing techniques, the period of the planet is simply the time it takes for the observable (e.g., the red-to-blue-to-red shift for the radial velocity) to repeat. For direct imaging, then we can simply observe how long it takes for the planet to move around its star once.
Semi-Major Axis (AKA Distance from the Star): The distance of the planet from the star relies upon first knowing the mass of the parent star. This is generally done through models of stellar evolution. Based upon the light that the star emits, we can fit this to models to determine how massive the star is pretty accurately. Once this is known, the full Newtonian form of Kepler's Third Law can be used to derive the mass of the planet:
![]()
In this equation, P is the period of the planet, G is the gravitational constant, r is the distance separating the two bodies, M1 is the mass of the star, and M2 is the mass of the planet (which is generally set as 0 relative to the star). G is the gravitational constant, as in Newton's Universal Law of Gravitation.
Mass: The mass of the planet is derived from knowing its period of rotation, the acceleration of the star due to the planet's tug, and its distance from the star. Newton's Law of Gravitation can then be used to determine the planet's mass. Because the acceleration due to the planet is needed, the mass can only be determined from the radial velocity technique. However, once a planet has been detected by another method, astronomers can go back and measure the planet's pull on its star via the radial velocity method and so derive the planet's mass.
Radius and Density: This is generally only able to be done for direct imaging (if we can resolve the planet's disk, then its actual radius can be determined) and transiting planets. For transiting planets, the fraction of light that is blocked by the planet is directly related to the size of the planet's disk relative to the star's disk. Since the area of a circle is simply A = π·r2, then the radius of the planet is the square-root of the fraction of light blocked times the star's radius. The star's radius is determined the same way as the star's mass - from models of stellar evolution based upon the star's light.
Once the radius of the planet is determined, then the density of the planet is just its mass divided by its volume (ρ=M/V=M/(4/3·π·r3)).
Eccentricity: The eccentricity of a planet can generally be determined from the radial velocity technique. While the color shifts from redder light to bluer light are regular, they will only be a "perfect" even wave if the planet is on a circular orbit. If, for example, the star's light spends a longer amount of time being redder than normal, then we know that the planet is taking a little longer going away from us than it is coming towards us. Due to Kepler's Second Law of Planetary Motion, we can then estimate the planet's eccentricity.
Orbital Inclination: This is generally only possible to determine for transiting planets. Hence, the very few inclinations that are known are fairly close to 90°. Note that this is just relative to Earth, and so it really has no importance to the planet's system itself.