What's Known About Exoplanets
Overview
Exoplanets are planets that are outside of our solar system, generally orbiting another star. To-date (mid-2008), there are approximately 300 known exoplanets. For most of them, due to the manner in which they have been detected, we know many of their orbital characteristics (the planet's year, distance from parent star, and eccentricity) as well as mass. For the very special case of transiting exoplanets, astronomers have also been able to determine some estimates of the composition of their atmospheres.
One of the overriding features that you will see in the first two sections on this page - Orbital Characteristics and Mass - is that most of the known exoplanets are large and orbit very closely to their parent stars (hence having a short period). This is mainly due to the biases in the various methods of detection: It is much easier to find a large planet that orbits close to its host star than it is to find a small planet that orbits far away.
In addition to information about exoplanets, there is also information that we know about the host star. Knowledge about the host star is much easier to derive because the star is so much brighter than the planet, but there are some important trends about the stars that are presented below.
Orbital Characteristics
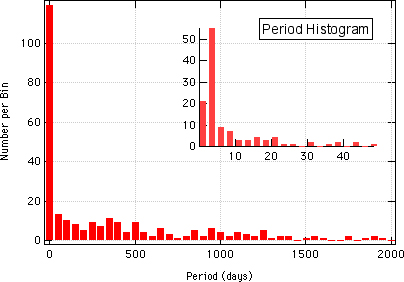Period: The "period" of a planet is the time it takes to orbit its parent star, in other words, the planet's "year." The reason that astronomers generally don't use the term "year" is that it is often confused with Earth's year, 365.24 days.
The graph on the right of known exoplanet periods shows one histogram of nearly all known periods (up to 2000 days, or about 5.5 Earth years, or about 0.5 Jupiter year). It also shows, inset, an expansion of the bin that is on the far left of the graph (0-50 days). The reason for this inset is to show the structure within that bin.
The obvious conclusion from this graph is that nearly 50% of known exoplanets have a period of less than 50 days (note that Mercury's year is about 88 days). Over 20% have a period of just 4 days or less. This means that the planets orbit around their parent stars very quickly, but it also means that it doesn't take too long to detect them. If their period is only 4 Earth days long, then astronomers just have to monitor the star for a week or less before they can detect the planet. Hence there is a very large bias towards finding exoplanets with very small periods, and it is likely that the known exoplanets are not representative of the vast majority that exist.
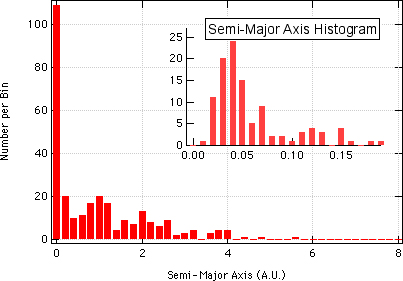Semi-Major Axis: Semi-major axis is a term that astronomers use to mean "radius of orbit." Using "radius of orbit" or "orbital radius" isn't entirely precise, however, because nearly every body in space orbits on an ellipse, having an eccentricity (see the sub-section below) greater than 0. The term "semi-major axis" is one-half of the longest line that goes through the center of an ellipse ("major axis" would the the entire length of the line), while the "minor" axis is the shortest line that goes through the center of the ellipse. By just indicating the semi-major axis and the eccentricity of an ellipse, the semi-minor axis can be derived.
The second graph shown at the right is a set of histograms of the semi-major axis of known exoplanets. Except in cases of direct imaging, the semi-major axis is a derived quantity rather than one that is directly observed. It relies on estimating the mass of the parent star. With that, then Kepler's Third Law of Planetary Motion can be used to derive the semi-major axis:
In this equation, P is the period of the planet, G is the gravitational constant, r is the semi-major axis, M1 is the mass of the star, and M2 is the mass of the planet (which is generally set as 0 relative to the star). G is the gravitational constant. So once the period (as described above) is known and the mass of the parent star is estimated, then the above equation can be solved for r and the semi-major axis determined.
Because this is derived almost directly from the period and because most searches for planets are focused on Sun-like stars (hence M1 being nearly the same), the graph on the right looks nearly identical to the graph of the period.
Most planets orbit very close to their host stars. Note that 1 A.U. (astronomical unit) is the distance between the Earth and Sun. So almost all of the known exoplanets orbit 20 times closer to their host star than Earth does, and over 6 times closer than the planet Mercury. Because of this, they are very hot, which is part of why most exoplanets are referred to as "Hot Jupiters."
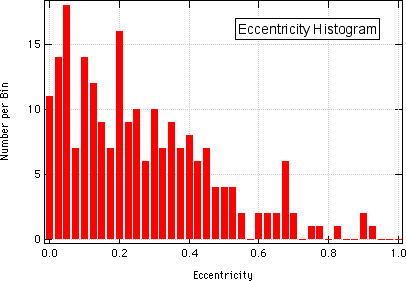Eccentricity: "Eccentricity" is a measure of how much an orbit is elongated relative to a perfect circle. A circle has an eccentricity of 0. In order for an object to actually be on a bound orbit, the eccentricity must be less than 1.
In general, it is assumed that objects will assume a generally circular orbit. Almost all of the planets in our solar system have a fairly small eccentricity, Earth's being 0.017 and Jupiter's 0.049. The planet with the largest eccentricity is Mercury at 0.209.
With these numbers in mind, over 50% of exoplanets have an eccentricity of about Mercury's or smaller. Fairly few have eccentricities larger than 0.5. These numbers are, in general, not very surprising to astronomers, for there is no observational bias towards finding planets with a greater or smaller eccentricity. Hence, what we observe is likely to be a reasonable representation of eccentricities of other exoplanets, with probably a few more on the lower end than we have observed to-date.
Mass
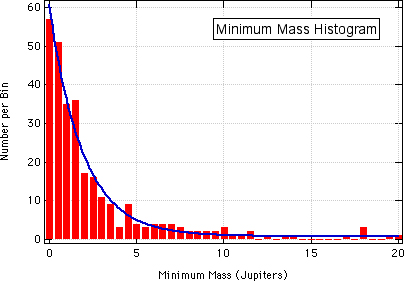The mass of exoplanets is a difficult quantity to determine, for it is another derived quantity as opposed to one that we can observe directly. The first point that needs to be addressed, however, is that except in the case of transiting exoplanets, we can only estimate their minimum mass, or a quantity that's often written as M·sin(i) where M is the mass of the planet and i is the inclination (tilt) of the planet's orbit relative to Earth.
This is because when we measure the tug of a planet on its parent star, we measure a smaller quantity than the real effect because the planet is tugging both "away" or "towards" us, but also a little bit "up" or "down," which is a motion that we cannot measure. Hence why the main technique for observing exoplanets is called the "Radial Velocity" -- we can only measure the velocity of the star radially towards and away from us.
Although this would appear to be an important complication, astronomers generally assume that the orientation of orbits is random, and they apply various techniques to estimate, from M·sin(i), what the true distribution of masses is. An example is Zucker & Mazeh (2001). Because these involve a fair amount of math, I will simply present the M·sin(i) data here as opposed to estimating the true distribution.
From the histogram shown on the right, it should be fairly clear that the smaller the mass, the more exoplanets are known. However, this is deceiving (as the period and semi-major axes plots were) because of our detection limits. We still have yet to find an Earth-mass planet, but as more planets are found, they continue to be smaller.
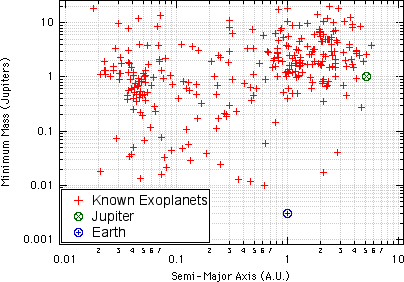However, there are many planets that are as large as or larger than Jupiter. This is the second half of the reason that many exoplanets are referred to as "Hot Jupiters" -- they orbit very close to their parent stars, and they are very large.
The second graph in this section, shown on the right, illustrates effectively "where we are" in finding both Earth-like and Jupiter-like planets. The graph is a logarithmic scatter plot showing the mass (in Jupiter masses) on the vertical axis and the semi-major axis (in A.U.s, or the Earth-Sun distance) on the horizontal axis. This graph makes it pretty clear that many planets are these "Hot Jupiters," but it is also clear that we are still unable to detect an Earth-mass planet. This is again due to our observational biases in detection methods: It is much easier to detect a massive planet close to its parent star than a small planet far away from its parent star.
Composition
Except for theoretical models, most of what is known about extrasolar planetary atmospheres is from the planet HD 209458b (the planet orbiting star HD 209458). This planet was first discovered by the radial velocity method, and it was then discovered in 2000 to also be a transiting planet. As discussed in the Transit Method subsection of the "Finding Exoplanets" page of this site, a transiting planet is important from other methods of observation because a little bit of the host star's light will filter through planet's outer atmosphere, and the planet's atmosphere will absorb certain wavelengths of light that allow us to determine what its composition is.
Currently, we know that this planet's atmosphere is escaping from the planet. Most of this material is simple hydrogen. However, both oxygen and carbon have also been observed escaping from the planet's atmosphere. In addition to this, sodium has been observed to be present within the atmosphere, but it has not been observed to be presently escaping.
The estimated escape rate today is greater than or approximately equal to 107 kg/sec. Over the course of 1 Earth year, the planet will lose about 3.2·1014 kg of material. That may seem like a lot, but it's only about 10% of the mass of Mars' smallest moon, Deimos. It would take 200,000,000 Earth years for the planet to lose as much mass as our own moon, which weighs only 0.004% as much as Jupiter. Since this planet is about 69% the mass of Jupiter, it would take about 4 trillion years for the planet to effectively disintegrate at the current rate. In other words, this is an incredibly negligible amount of material that is presently escaping.
Stellar Type and Metallicity
As the number of known exoplanets has continued to rise, astronomers looked for trends - based upon known exoplanets - in order to better predict where in the sky, or around what stars, to look for future discoveries.
One of the first ways that astronomers narrowed their field is that they generally only look for exoplanets around Sun-like stars, of stellar type F, G, and K (our star is a type G star). The justification for this is that the ultimate goal is to find planetary systems like our own and that are capable of supporting life. In addition, stars that are much larger and hotter than the Sun generally go through their supply of nuclear fuel too quickly for (we believe) life to develop. Stars much smaller and cooler than the Sun hardly put out any heat, so any planet that would support life as we know it would need to orbit very close to the parent star.
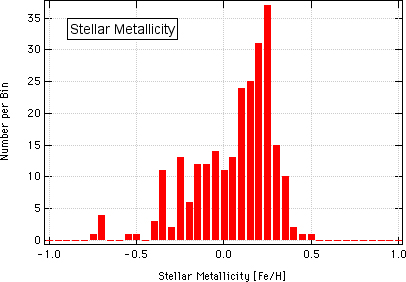The second way that astronomers have, in the last few years, narrowed their search is by looking at stars that have a high metallicity, meaning that they have a lot of iron relative to the Sun. First off, to explain the terminology a little, astronomers are generally not chemists, and as such they don't think of a "metal" as a chemist would or as most people do in every-day life. To astronomers, or at least to astronomers that study stars, a "metal" is an element that is heavier than helium. So oxygen is a metal. Aluminum is a metal. Uranium is a metal.
Astronomers measure the metallicity of stars by measuring the amount of iron that is in a star relative to the amount of hydrogen. This is written as [Fe/H], and it is pronounced, "F-e-on-h." The definition of it is:
The circle with a dot in the center is the astronomical symbol of the Sun. With this equation, you can see that the Sun is defined as [Fe/H] = 0. A star that is metal-poor relative to the Sun will have a negative value, and a star that is metal-rich relative to the Sun will have a positive value.
With this definition in mind and the histogram on the right, it is fairly clear that stars around which we have discovered exoplanets are particularly rich in metals; the average value is [Fe/H]=0.077. It should be noted here that this is NOT indicative of the stars that have been searched up until this point - in general, stars that have been searched have a metallicity close to the Sun, with an approximately even amount of metal-poor and metal-rich stars (see Fischer & Valenti, 2005).
It has been suggested that this is due to a preference of planet formation to take place more easily in regions with denser materials. However, this conclusion is still fairly preliminary, as most studies that have modeled this effect restrict the stellar metallicity-planet formation correlation to systems that will form a Jupiter-like planet with an orbital period of less than 4 years (placing it a little outside of Mars' orbit).
If this holds to be true in future studies, however, it has implications for planet formation in the early days of the Universe. Because heavier elements are the result of both nuclear fusion during stellar lives and supernova explosions, the earliest generations of stars would be almost completely composed of hydrogen and helium with no heavier elements (other than primordial lithium and beryllium). With a tremendous deficit of metals, planets likely would not have formed around the first few generations of stars.